Elliptic Curve Cryptography Calculator

You can enter your own input to use the ECC calculator. solves the discrete logarithm to the base . That is, it finds the value such that on . computes the number of points on the curve. computes the number of points in the subgroup generated by . That is, is the symbol for order. You can also generate random elliptic curves mod , and random elliptic curves with a prime number of points (not necessarily ).
For higher-degree binary fields for ECC calculations, see the following stand-alone Python program. You'll need to make sure your irreducible polynomial is actually irreducible. Otherwise, strange things may or may not happen.
Modulus
Elliptic Curve
Generator
Point
Point
Exponent

Output

hi

Elliptic Curve Cryptography Overview

RSA is mathematically very simple, but unfortunately, factoring integers is not quite as hard as we would like (that is, there are sub-exponential time algorithms for this task), which means keys with thousands of bits need to be used. Elliptic curve cryptography allows us to get away with keys that are "only" a couple hundred bits long, which makes computations faster (even though RSA calculations would make things much faster if the same key sizes could be used to achieve the same levels of security). For example, 3000-bit RSA keys are needed to match the security of 128-bit AES, while ECC can get away with 256-bit keys. To match AES-256, RSA requires 15000-bit keys, while ECC only requires 512-bit keys!

An elliptic curve is the set of points in the plane satisfying for fixed parameters and . The coordinates can come from any field, such as the real numbers or rational numbers. For cryptographic purposes, however, we will use the integers mod (for ) and binary fields (fields with elements for some ). We also require that . This ensures that the right side of the equation has no repeated roots (this is similar to a quadratic equation having no repeated roots being equivalent to ).

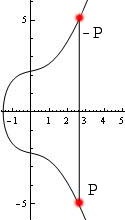
Any elliptic curve also includes a point at infinity, which we will denote as (some references denote it as ). This is a formal identity element, which we will get into below. Here are two graphs of elliptic curves over the real numbers (mod p, you can just visualize them as a discrete set of points).

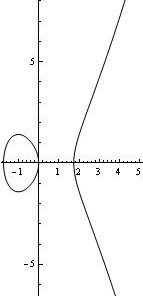
Elliptic curves form what is called a group. What this means for us is that we can take two points on the curve and add them to find a third point on the curve. Addition is not simply pointwise addition. The basic idea is that we draw a line between the two points. This line will intersect the curve in a third point. We then reflect across the -axis (notice that the curves are symmetric across the -axis). This point is the result of the addition.

There are several cases. The first case is adding two distinct points and . This is the idea described above. A very similar case is adding a point to itself: in this case, we draw the line tangent to the curve at , which intersects the curve in one more point, and we follow the same procedure as above. The other case is when we are adding a point to its reflection across the -axis, in which case we define . This is the "identity" element. This last case has the subcase of when lies on the -axis since its reflection is itself.

You can think of this as intersecting every vertical line through the curve way off the graph both to the top and the bottom of what one can see. One way to summarize the addition rule is by saying iff , , and lie on the same line. See the images below for illustrations of elliptic curve point addition.

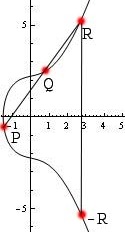
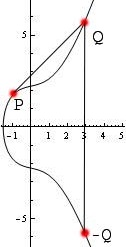
Here are the formulas for , where .

First the easy case. If , that is, (including the case ), then .

If , then , where $$x_3 = m^2 - x_1 - x_2, y_3 = m(x_1 - x_3) - y_1, m = \frac{y_2 - y_1}{x_2 - x_1}.$$

If , then , where $$x_3 = m^2 - 2x_1, y_3 = m(x_1 - x_3) - y_1, m = \frac{3x_1^2 + a}{2y_1}.$$

The term is simply the slope of the line between the two points. When , this is the usual slope formula. When , it is the slope of the tangent line to at and is computed using calculus. (It is not a coincidence that in this case it is the ratio of the derivatives of the two sides of the equation for .

Elliptic Curve Orders

The order of , denoted , is the number of points on . That is, the number of points satisfying . The order of the point , denoted , is the smallest integer such that . Note that divides . This is Lagrange's Theorem (very similar to Euler's Theorem).

This means to find the order of a point , we can factor , and find the smallest factor with , similar to finding the order of primitive roots mod . But how do we find the order of ? One inefficient way is to try all points and count how many of these points satisfy .

A better technique is to recall (see square roots in finite fields) that has solutions. This means we can compute the order of as $$|E| = 1 + \sum_{x=0}^{p-1} \left(1 + \left(\frac{x^3 + ax + b}{p}\right)\right) = p + 1 + \sum_{x=0}^{p-1} \left(\frac{x^3 + ax + b}{p}\right).$$

There are actually more efficient ways to do this, but we will not get into them here. One nice result is Hasse's Theorem, which states that . This means that , or .

So given a curve , how do we find a generator ? To find a point on , we can choose a value for , and check if has a square root mod . If so, we can use that square root as the -coordinate. This point may not generate all of , though. It's not always necessary for to generate all of , as long as is sufficiently large and not a product of small primes.

However, if we restrict ourselves to elliptic curves with a prime number of points (possibly different from the modulus ), it turns out any finite point (any point ) will generate . For this reason, we frequently insist that be prime.

Elliptic Curve Discrete Logarithms

Elliptic curve cryptography is based on the elliptic curve discrete logarithm problem, which is very similar to the classic discrete logarithm problem. In the classical case, discrete logarithms undo modular exponentation: that is, they extract the from the equation . In our case, modular exponentiation is written additively (since the operation is called point "addition," not "multiplication"): $$kG = \underbrace{G + G + \ldots + G}_\text{k terms}.$$

This exponentiation can be computed efficiently using modular exponentiation (that is, repeated doubling). For example, .

The discrete logarithm problem for elliptic curves is to solve . Note that the number lives mod . Also note that may not have a solution. (If you know group theory, could lie in the wrong coset.)

Elliptic curve cryptography has a couple of advantages. First, in the classical case, once you fix the prime , you have only one group to work with. In ECC, for a fixed prime , there are many elliptic curves mod to choose from. Secondly, the most efficient algorithm in the classical case, the index calculus, runs in sub-exponential time. There is no analog of this algorithm for ECC because it relies on factorization of integers mod . There is no known way to factor points into a product of "primes" (or a sum since we use additive notation with elliptic curves). (Caveat: there are curves called supersingular curves for which it is possible to transform EC discrete logs into classical discrete logs and solve them more efficiently. Such curves should be avoided.)

As a result, the best known algorithm for EC discrete logs is Pollard's Rho Algorithm, which operates very similarly to Pollard's Rho Algorithm in the classical case. This algorithm takes time, where . This is still exponential time since the key-size is exponential in the number of bits in the input. That is, if , then .

Diffie-Hellman works in almost exactly the same way in the elliptic curve case as in the classical case. First, an elliptic curve mod is agreed on. Aaron chooses a secret integer and sends to Blumenfeld. Blumenfeld chooses a secret integer and sends to Aaron. Aaron and Blumenfeld can then compute . In this case, is a point, so they agree on some algorithm to extract a key out of the point. For example, the -value could be used.

There are also cryptosystems (such as ECIES) and digital signature algorithms (such as ECDSA) using elliptic curve cryptography. These both are based on the hardness of the discrete logarithm problem. We won't get into the details of these algorithms here; Diffie-Hellman provides enough context for EC discrete logarithms.

Elliptic Curve Cryptography over Binary Fields

Also frequently used in cryptography are elliptic curves over binary fields. These curves take on a slightly different form: , with the restriction that (this ensures the right side of the equation has no repeated roots). Here, , and are polynomials mod 2, not integers. For example, a curve might be represented by the equation .

Here are the formulas for , where .

First for all points . Secondly, inverses are given by the formula .

If , then , where $$x_3 = m^2 + m + x_1 + x_2 + a, y_3 = m(x_1 + x_3) + x_3 + y_1, m = \frac{y_2 + y_1}{x_2 + x_1}.$$

If , then , where $$x_3 = m^2 + m + a, y_3 = x_1^2 + mx_3 + x_3, m = x_1 + \frac{y_1}{x_1}.$$

In the ECC calculator above for binary fields, we don't support what are called supersingular elliptic curves (which take the form . There are reasons to avoid supersingular elliptic curves, and the addition formulas for them differ.

Why do we sometimes use binary fields instead of prime fields? The main reason is that we can do the computations very efficiently: a polynomial mod 2 can be represented as a sequence of bits. For example, can be represented as . Polynomial addition can be implemented using XOR, and polynomial multiplication can be implemented using a combination of bit-shifts and XOR.

One difference with the binary case is no curves have prime order. This is because the order of a curve is always even. This can be seen by the fact that the inverse of a point is . In particular, is its own inverse: . The order of this point is 2, which must divide the order of the curve. But is guaranteed to be on the curve? Yes, as long as has a solution. But every element of a binary field has a square root, so this point is always on the curve. As a result, we often talk about "almost prime" orders, which means that the order of the curve is for some small value of (say, ) and some prime .

Projective Coordinates

One problem with using affine coordinates (i.e., the normal coordinate system we've used throughout this page) is that we need to do a field division every single time we add points. This can be costly when doing "exponentiation" (i.e., point multiplication). For example, to compute , we require 6 point additions, and thus 6 field divisions. Of course, it's possible to turn this into only 5 additions by writing , but field divisions are much more expensive than field additions and multiplications. (Here, "field division" means division mod p, or polynomial long division in a binary field.)

So it's possible to use what are called projective coordinates. Specifically, we identify a point with the point for any . We can then identify a two-dimensional point in affine space with a three-dimensional point in projective space by the map .

It turns out the point addition formulas in projective coordinates don't involve any field divisions, so when computing , we only need to do one division at the very end (instead of divisions). In practice, this results in a roughly 35% speed-up. One other advantage is this gives us a nice way to represent the point at infinity in the computer: (there are reasons it takes this specific form; we won't go into the details here).

Lenstra's Algorithm for Integer Factorization

There is an algorithm that uses elliptic curves for factoring integers, due to Lenstra. It is not applicable to elliptic curve cryptography per se, but it is interesting and is applicable to other cryptographic schemes such as RSA, so we describe it here. The idea is to factor by coming up with a random elliptic curve , along with a point on and an integer . This is not actually an elliptic curve because the integers mod do not form a field. That is, when computing slopes while adding points, we need to do an inversion mod . This is only guaranteed to work when is prime.

So pretend we do have a legitimate elliptic curve and try to compute . If we can't do a division, it's because . If the gcd is = n, we learn nothing, but if the gcd is < n, we have found a non-trivial factor of n. If we fail, we can choose a different curve, or a different base point. One common choice for k is for some relatively small value of . We can compute by computing , etc.

In order to choose and , we cannot just choose random values for , and compute as since computing square roots mod a composite integer is hard. Instead, we can choose randomly, and compute .

We can think of this in the case as working because the number we're trying to divide by is nonzero mod p, but zero mod q (or vice versa). For example, let's try to factor using this algorithm. Randomly choose . This gives . Thus . Let .

We first compute : the slope was , and is invertible since . But when we try to compute , we encounter problems. Specifically, computing is fine since the slope is , and again, is invertible since . So we compute . But when computing , we observe the slope is . But we cannot invert since . We have thus found the factor , and the other factor is .

This is a common idea with factoring algorithms: try to do something clever and extract a non-trivial factor using a gcd calculation, which can be done very quickly (in logarithmic time). In our case, 14 was invertible mod 13, but not mod 7. Even though we didn't know the factorization, we were able to extract a factor using the gcd.