An Amusing Quad Tree Problem
Given a quad tree for storing (not necessarily horizontal) line segments, if we insert 2 segments into an initially empty tree, give an upper bound on the number of leaves. Be as precise as possible.
One thought is to use horizontal segments placed as close together as possible. This gives leaves on each of the top two rows, plus leaves below it, plus , and so on, all the way down to .

This sums up to $$2^h + \sum_{i=1}^h 2^i = 2^h - 1 + \sum_{i=0}^h 2^i = 2^h - 1 + 2^{h+1} - 1 = 3 \cdot 2^h - 2.$$
(Vertical line segments are the same. Just rotate your head.)
Another possibility is two parallel diagonal line segments.

Looking at the picture, it's not too hard to convince yourself that we have a recurrence relation $$a_h = 2a_{h-1} + 2.$$ Here, is the number of leaves after subdividing times. The solution to this recurrence is also $$a_h = 3 \cdot 2^h - 2.$$ How can we come up with this formula? Well, this type of recurrence isn't super easy to solve, but if we assume (this is basically guesswork) that the solution takes the form , we can plug in 0 and 1 and get . This solves to , and we're done.
In fact, another argument is to transform this into the first picture: imagine bubbling the smaller squares to the top and the larger squares to the bottom. We would get essentially the same picture as the first quad tree. It's not a coincidence that these two constructions give the same exact number of leaves.
But can we do better? Notice above the two lines only intersected 2 of each set of 4 quadrants along the middle (the drawing isn't perfect). What if the lines intersect 3 of them? See the following image:
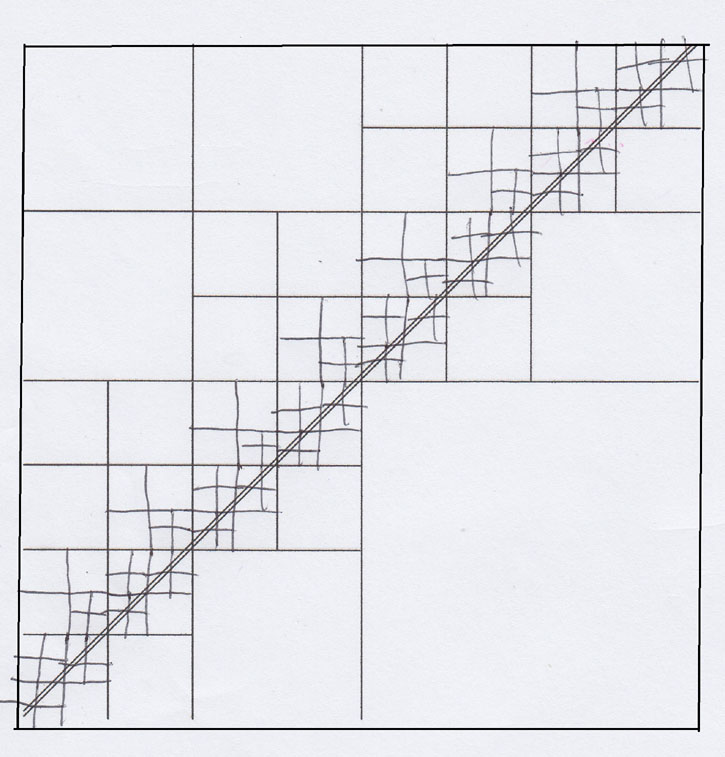
This one looks much nastier to figure out. The sequence of values we get for is . A very useful website when working on combinatorial problems is OEIS (Online Encyclopedia of Integer Sequences). See the link to this sequence here. It's usually not a coincidence when our sequence matches up with a sequence that came up in a completely different context.
Reading that page, we see that the solution is (which is greater than for ). This can be derived from the recurrence .
Stare at the picture long enough to convince yourself that this recurrence holds. Here is a hint as to why this recurrence holds:
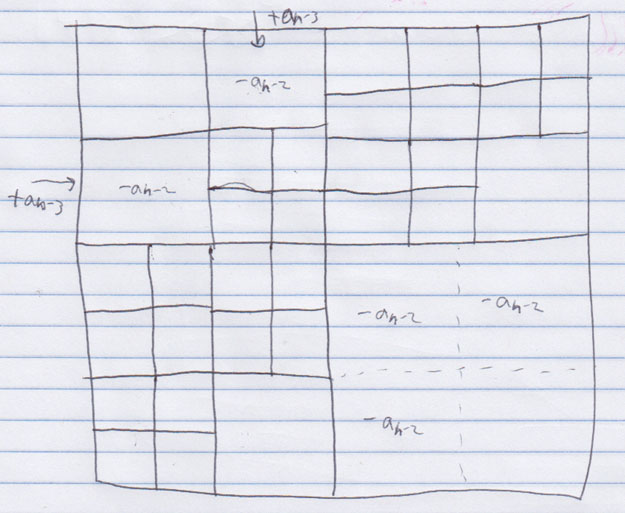
This material is far beyond the scope of this class, but may be of interest to you if you like math. This technique is pretty similar to solving certain types of differential equations if you're a math major.
We write what's called the characteristic polynomial, which is in this case, and find the zeroes of it. For each root , the solution will have a term . If there is a double root, we'll also have ; if there's a triple root, , etc.
How do we find the zeroes of ? We could use the formula for a cubic, which is similar to the quadratic formula, only way uglier. A better approach is the rational root theorem: it says if there's a rational root, the numerator will be plus or minus a factor of the last coefficient (2), and the denominator will be a factor of the first coefficient (1). So the possibilities are . (This theorem excludes irrational roots, like , etc.)
Plug 2 into and get 0: this means is a factor. Do polynomial long division to obtain .
This means the sequence will have a closed-form formula of $$a_h = c_02^h + c_11^h + c_2h1^h = c_02^h + c_1 + c_2h.$$ We have the initial conditions . Thus . You can perform a little algebra and obtain . Therefore, $$a_h = 6 \cdot 2^h - 3h - 5.$$
(This is exactly how one computes the closed-form formula for the Fibonacci sequence. See here for the details of the computation, along with more details on the general technique for solving linear homogeneous recurrence relations with constant coefficients.)
In fact, an easier recurrence to see is $$a_h = 2a_{h-1} + 1 + 13 + 3(h-5) = 2a_{h-1} + 3h - 1$$ for with . While this recurrence is easier to see, it's harder to solve. If you assumed the solution took the form , you would obtain the equations , which has the solution , giving the solution , as before.
But is this the best we can do? It certainly seems like it. After all, if two parallel lines intersect a node, they can't possibly intersect all four children (do you see why?). Nevertheless, the first two solutions are pretty good. Not optimal to the level of perfect constants, but all are , which is the point of this problem.